Représentation des entiers naturels
Notion de bases de numération
Compter en base 10
Lorsqu’on compte, on utilise 10 chiffres, allant de 0 à 9. Une fois que l’on a épuisé l’ensemble de ces chiffres, on ajoute une colonne des dizaines, puis on compte, pour chaque dizaine allant de 0 à 9, le nombre d’unités allant de 0 à 9. Une fois atteintes les 9 dizaines + 9 unités, on passe aux centaines, etc.
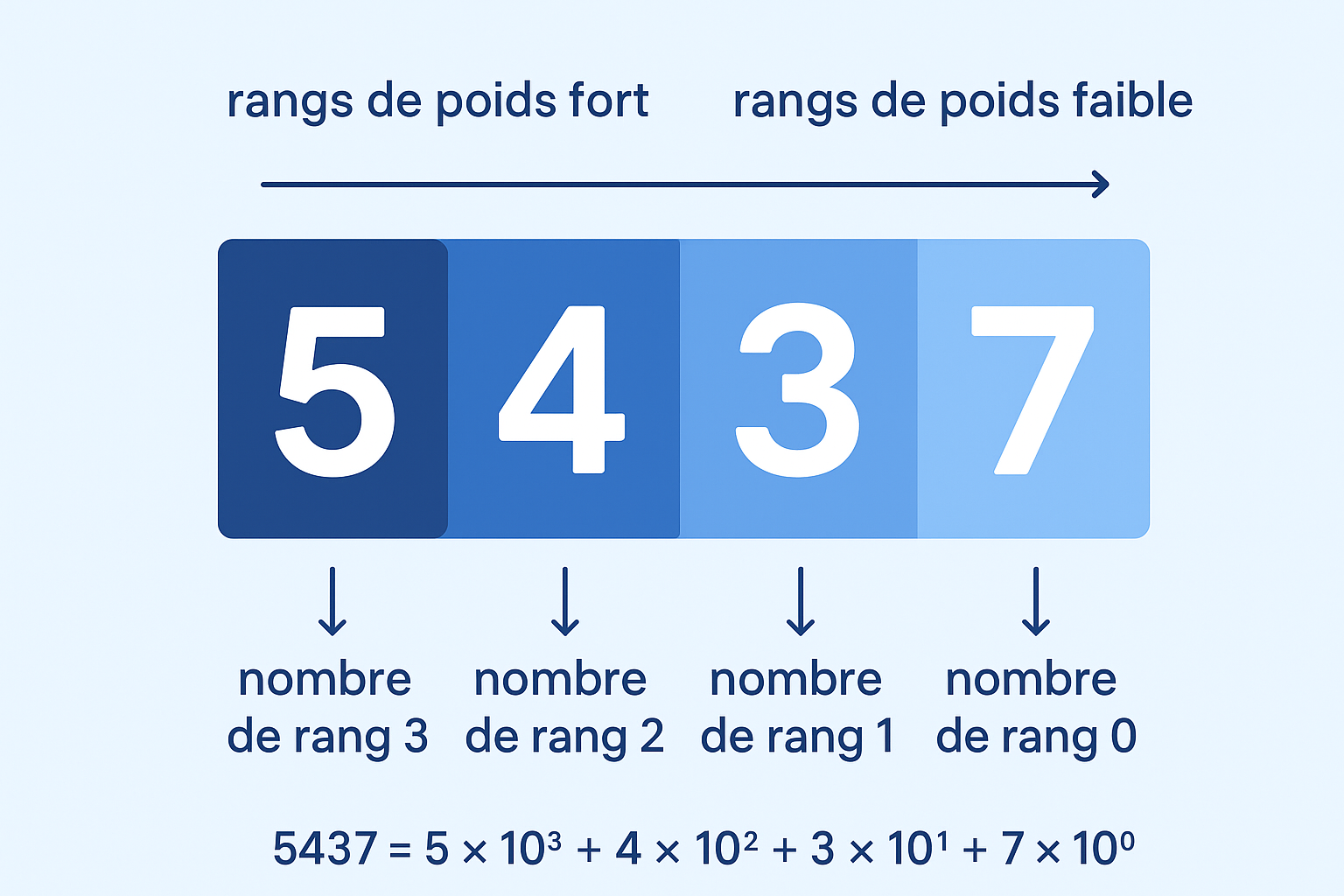
Pour représenter ce nombre, on juxtapose les chiffres ayant chacun un rang (centaine, dizaine, unité, etc.) égal à une puissance entière de la base de numération (10², 10¹, 10⁰, etc.). Les chiffres s’écrivent de gauche à droite, par valeur décroissante de leur poids :
Compter dans une autre base
Comment ferait-on si on disposait de moins de chiffres, par exemple seulement 4, comme les shadoks ? Pour simplifier, supposons qu'il s'agit des 4 chiffres 0, 1, 2 et 3 (au lieu de ga, bu, zo et meu).
La réponse est simple, on procède exactement de la même manière :
- On commence par les unités : 0, puis 1, 2 et 3.
- Ensuite, on ajoute 1 au nombre de dizaines, et on recommence : 10, 11, 12, 13, et ainsi de suite : 20, 21, 22, 23 puis 30, 31, 32, 33.
- On passe maintenant aux centaines : 100, 101, 102, 103, 110, 111, 112, 113, 120, 121, 122, 123, 130, 131, 132, 133, 200, 201, ...
Au final, chaque nombre en base 10 possède un équivalent en base 4 :
| Base 10 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base 4 | 0 | 1 | 2 | 3 | 10 | 11 | 12 | 13 | 20 | 21 | 22 | 23 | 30 | 31 |
Base 2 : Le système binaire
En raison de la composition physique des ordinateurs (circuits électriques et transistors ayant seulement deux états possibles), on ne peut représenter les données en mémoire qu’à l’aide de deux symboles 0 ou 1.
Compter en base 2
Le principe est exactement le même qu'en base 10 ou 4 : on se contente d'ajouter un nouveau rang lorsque tous les rangs précédents sont à 1.
Vocabulaire
Un nombre en base 2 (10110101 par exemple) est souvent appelé un mot binaire, et un chiffre est appelé un bit.
Un mot de 8 bits est appelé un octet. En informatique, les données sont souvent formatées par multiples d’octets (8 bits, 16 bits, 32 bits, etc.).
Dans un mot binaire, le bit le plus à gauche est appelé le bit de poids fort, et le bit le plus à droite est appelé bit de poids faible.
| Décimal | Binaire |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
Combien de valeurs peut-on coder sur n bits ?
En base 10, on peut écrire 10 nombres différents avec un seul chiffre, 100 (10 x 10 = 102) nombres différents avec 2 chiffres, 1000 (10 x 10 x 10 = 103) nombres différents avec 3 chiffres, et ainsi de suite. En réalité, cela fonctionne avec toutes les bases.
À retenir
Sur N bits, on peut coder 2N valeurs différentes, entre 0 et 2N-1
Convertir de la base 2 vers la base 10
Pour convertir un nombre depuis une autre base vers la base 10, il suffit de multiplier chaque chiffre par son poids et d’additionner l’ensemble :
(1101)2 = 1 x 2³ + 1 x 2² + 0 x 2¹ + 1 x 2⁰ = 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1 = (13)10
Convertir de la base 10 vers la base 2
Pour convertir un nombre en base 10 vers la base 2, il faut effectuer des divisions successives. On divise le nombre de départ par 2, on note le reste à droite, puis on recommence avec le résultat, en notant les restes de droite à gauche :

Base 16 : Le système hexadécimal
D’autre part, pour faciliter la lecture des nombres binaires, on utilise la représentation hexadécimale (en base 16), dont l’alphabet comprend les 10 chiffres de la base 10, puis les lettres allant de A à F.
Convertir de la base 16 vers la base 10
Le principe est le même que pour la base 2 :
(3F)16 = 3 x 16¹ + 15 x 16⁰ = 48 + 15 = (63)10
Convertir de la base 10 vers la base 16
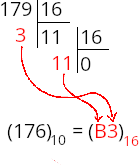
Là encore, le principe est le même que pour la base 2, il suffit de faire des divisions successives, mais par 16. Et si le reste est supérieur à 10, on le remplace par la lettre correspondante :
Convertir entre la base 2 et la base 16
Il s'agit de l'un des avantages de la base 16 : Le passage entre la base 2 et la base 16 est très simple.
Il suffit de regrouper les bits par 4, puis de convertir chaque groupe en héxadécimal, en les gardant dans le même ordre. Et cela marche dans les deux sens :
(0100 1101 0010 1100)2 = (4D2C)16
(FF34A2)16 = (1111 1111 0011 0100 1010 0010)2
| Décimal | Binaire | Hexadécimal |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 10000 | 10 |
| 17 | 10001 | 11 |
Remarque
Attention, il faut bien veiller à garder des groupes de 4 bits. On ajoute des 0 devant si besoin.

