Représentation des nombres réels
Remarque
Pour parler des nombres réels en informatique, on utilise souvent le terme flottants issu de l'anglais float. On utilise ce terme car, comme nous le verrons par la suite, c'est ainsi que les nombres réels sont représentés en mémoire.
Principe et conversions
Pour représenter la partie décimale d'un nombre, on peut utiliser exactement le même principe que pour représenter sa partie entière :
(11,1011)2 = 1 x 21 + 1 x 20 + 1 x 2-1 + 0 x 2-2 + 1 x 2-3 + 1 x 2-4
(11,1011)2 = 2 + 1 + 0.5 + 0 + 0.125 + 0.0625
(11,1011)2 = (3,6875)10
Cela signigie que pour faire la conversion décimal → binaire, on peut procéder par multiplications successives :
On souhaite convertir 0,6875 en binaire :
- On multiplie 0,6875 par 2 : 0,6875 x 2 = 1,375. On garde la partie entière pour le résultat final, et on recommence avec la partie décimale :
- On multiplie 0,375 par 2 : 0,375 x 2 = 0,75.
- On multiplie 0,75 par 2 : 0,75 x 2 = 1,5.
- On multiplie 0,5 par 2 : 0,5 x 2 = 1,0.
On lit le résultat du haut vers le bas : (0,6875)10 = (0,1011)2
Pourquoi "flottants" ?
De manière générale, en base 10, on appelle nombre à virgule flottante un nombre écrit sous la forme a x 10 b. C'est la notation scientifique utilisée en physique par exemple (avec a ∈ [1,10[). a s'appelle la mantisse, et b l'exposant.
En informatique, on utilise la même notation pour stocker les nombres. On part du principe que tous les nombres sont écrits sous la forme ±0,mantisse x 2exposant, et on ne conserve que le triplet (signe, mantisse, exposant). Par exemple, (11,1011)2 peut aussi s'écrire +0,111011 x 22.
La seule contrainte est d'utiliser une norme pour que tout le monde soit d'accord sur le nombre de bits utilisés pour la mantisse et l'exposant.
Remarque
La norme principalement utilisée de nos jours est la norme IEEE-754 (lien vers sa page wikipedia).
Limitations
Il y a deux limitations majeures aux nombres flottants en programmation. Le premier est lié à la norme. Partant du principe que la norme utilisée est la norme double précision, on ne peut utiliser "que" des nombres allant jusqu'à 1,797 693 134 862 315 7 × 10308. C'est beaucoup, certes, mais pas infini.
Le second problème est plus génânt. Considérons l'exemple suivant. Suppons que l'on dispose d'un espace de 11 bits et convertissons les 3 nomrbes suivants : 0.1, 0.2 et 0.3
Conversion de (0,1)10 en binaire :
0,1 x 2 = 0,2 → 0 + 0,20,2 x 2 = 0,4 → 0 + 0,4
0,4 x 2 = 0,8 → 0 + 0,8
0,8 x 2 = 1,6 → 1 + 0,6
0,6 x 2 = 1,2 → 1 + 0,2
0,2 x 2 = 0,4 → 0 + 0,4 et on boucle à l'infini...
On obtient donc 0,00011001100
Conversion de (0,2)10 en binaire :
0,2 x 2 = 0,4 → 0 + 0,40,4 x 2 = 0,8 → 0 + 0,8
0,8 x 2 = 1,6 → 1 + 0,6
0,6 x 2 = 1,2 → 1 + 0,2
0,2 x 2 = 0,4 → 0 + 0,4 et on boucle
On obtient donc 0,00110011001
Conversion de (0,3)10 en binaire :
0,3 x 2 = 0,6 → 0 + 0,60,6 x 2 = 1,2 → 1 + 0,2
0,2 x 2 = 0,4 → 0 + 0,4
0,4 x 2 = 0,8 → 0 + 0,8
0,8 x 2 = 1,6 → 1 + 0,6
0,6 x 2 = 1,2 → 1 + 0,2
0,2 x 2 = 0,4 → 0 + 0,4 et on boucle
On obtient donc 0,01001100110
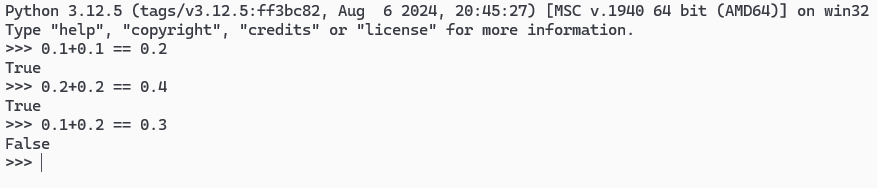
Faisons maintenant la somme (0,1) + (0,2) :

Attention !
On remarque que le résultat est différent de 0,01001100110, ce qui signifie que pour un ordinateur, 0,1 + 0,2 ≠ 0,3.
Pour faire simple, c'est dû au fait que la mémoire d'un ordinateur est limitée, et le nombre de valeurs comprises entre deux nombres donnés ne l'est pas. Il est donc virtuellement impossible de créer un système de représentation des données permettant de manipuler de manière fiable des nombres réels.
Conclusion
On peut représenter des nombres réels, et les utiliser pour faire des calculs avec une précision remarquable, mais il faut absolument garder à l'esprit qu'il s'agit toujours d'approximations, et il est impératif de se souvenir de ne jamais faire de comparaison d'égalité entre deux nombres flottants car les résultats sont imprévisibles.