Les Arbres

Structures hiérarchiques : pourquoi des arbres ?

Un arbre est une structure de données hiérarchique composée de nœuds reliés par des liens parent-enfant. On la rencontre partout : systèmes de fichiers, organisation d'entreprise, expression arithmétique, DOM d'une page web, etc.

Vocabulaire

• Une racine est un nœud sans parent.
• Une feuille est un nœud sans enfant.
• La taille d'un arbre est le nombre total de nœuds qui le constituent.
• Une arête est un lien entre deux nœuds.
• Un chemin est une suite d'arêtes reliant deux noeuds.
• La hauteur d'un arbre est la longueur (en arêtes) du plus long chemin racine ⟶ feuille.
• La profondeur d'un nœud est la longueur du chemin entre la racine et ce noeud

Exemple

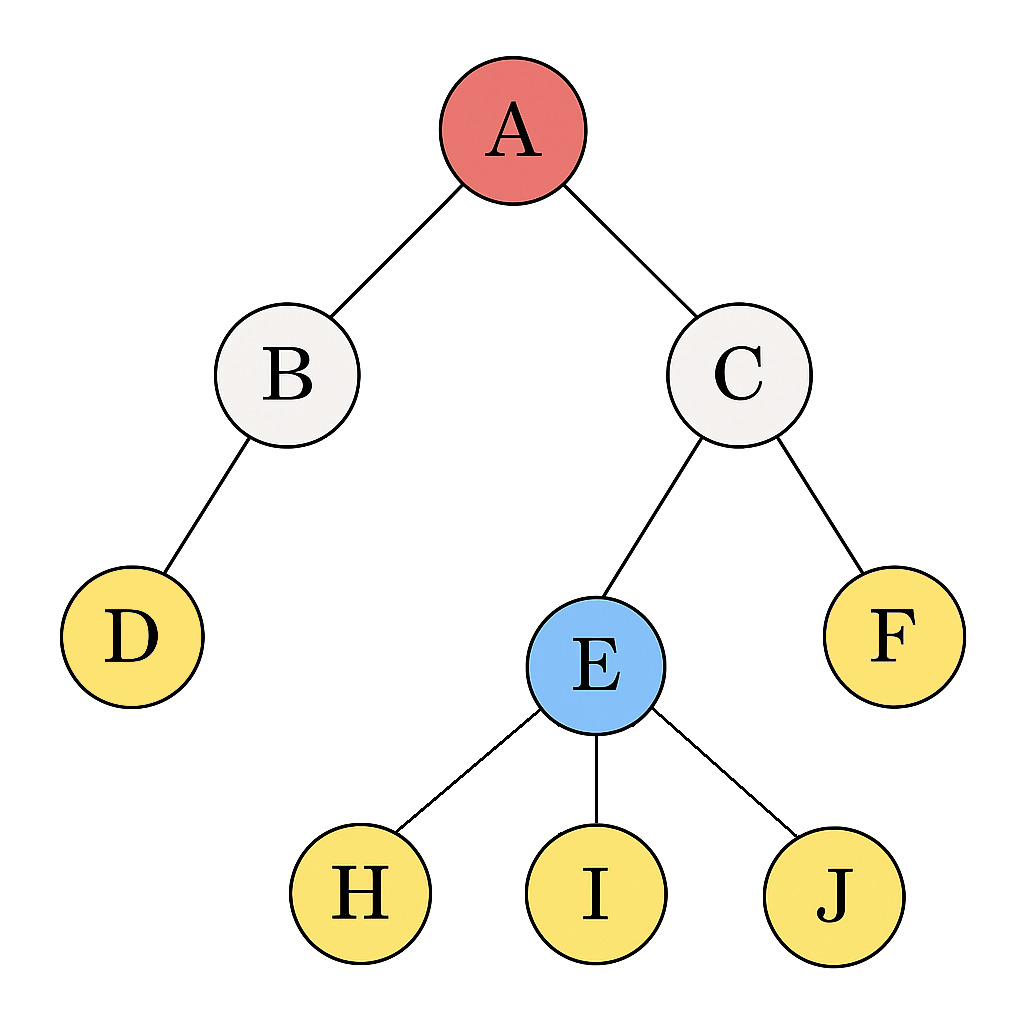
Le noeud A est la racine de l'arbre, les nœuds D, F, H, I et J sont des feuilles.
La taille de l'arbre est 9, la hauteur de l'arbre est 3, et la profondeur du noeud E est 2.

Remarque : On peut aussi considérer que la profondeur de la racine vaut 1, ce qui donne une hauteur de 4, et la profondeur du noeud E vaut alors 3.

Parcours d'un arbre

Parcourir un arbre signifie accéder à l'ensemble de ses noeuds, que ce soit pour les énumérer ou pour effectuer un traitement sur ceux-ci

Il existe deux types de parcours différents:

• En largeur, c'est à dire "étage par étage" : A, B, C, D, E, F, H, I, J.
• En profondeur, c'est à dire en épuisant chaque chemin jusqu'à une feuille avant de passer au suivant : A, B, D, C, E, H, I, J, F .

Implémentation d'un arbre en python

La programmation orientée objet est très adaptée pour implémenter un arbre en python. Il suffit en réalité de définir une classe représentant un noeud, avec par exemple un attribut valeur indiquant le contenu du noeud, et un attribut parent contenant le noeud parent :

Les arbres binaires

Un arbre binaire est un arbre dont les noeuds ont au plus deux enfants. On parle de sous-arbre gauche et de sous-arbre droit pour désigner les enfants d'un noeud, ainsi que tous ses descendants.

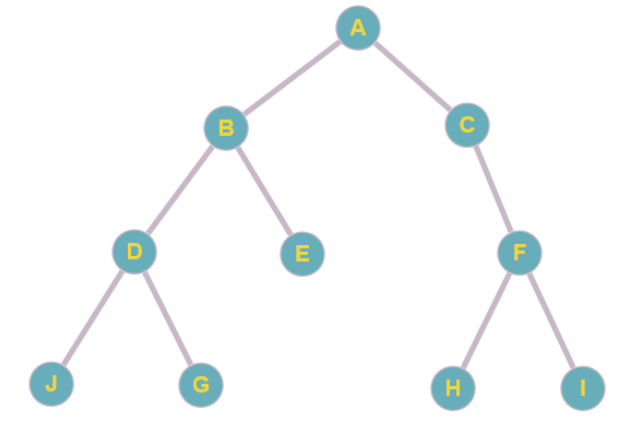
Parcours d'un arbre binaire

Comme pour n'importe quel arbre, on peut parcourir un arbre binaire en largeur ou en profondeur. Dans le cas du parcours en profondeur, on dénombre trois manières de procéder :

• Parcours en largeur : A, B, C, D, E, F, J, G, H, I
• Parcours en profondeur :
  • Préfixe, d'abord le noeud, puis son sous-arbre gauche, puis son sous-arbre droit : A, B, D, J, G, E, C, F, H, I
  • Infixe, d'abord son sous-arbre gauche, puis le noeud, puis son sous-arbre droit : J, D, G, B, E, A, C, H, F, I
  • Suffixe, d'abord son sous-arbre gauche, puis son sous-arbre droit, puis le noeud : J, G, D, E, B, H, I, F, C, A

Les arbres binaires de recherche (ABR)

Un arbre binaire de recherche est un arbre binaire dans lequel chaque noeud possède une clé (=une valeur associée), et pour chaque noeud, les clés de tous les noeuds de son sous-arbre gauche ont une valeur inférieure à la sienne, et les clés de tous les noeuds de son sous-arbre droit ont une valeur supérieure à la sienne.