Les Graphes

Structures relationnelles : pourquoi des graphes ?

Contrairement aux arbres qui imposent une hiérarchie stricte (un fils n'a qu'un seul père), le graphe est une structure de données permettant de modéliser des relations libres et complexes entre des entités.

Objectifs

Modéliser des situations concrètes (réseaux sociaux, routage, cartes).
Maîtriser le vocabulaire : sommets, arcs, arêtes, orientation, connexité.
Implémenter un graphe en Python via une matrice ou une liste d'adjacence.

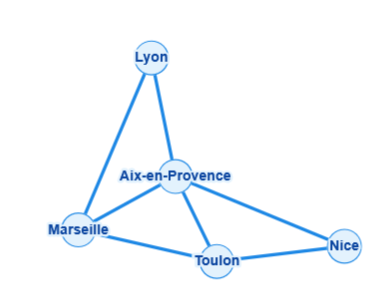
Exemple 1 : Réseau routier

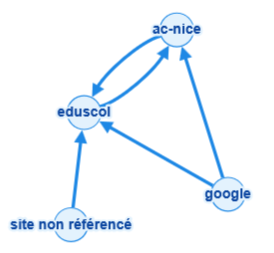
Exemple 2 : Réseau web

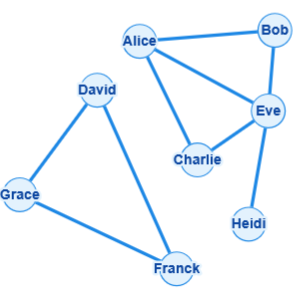
Exemple 3 : Réseau social

Vocabulaire technique

Les éléments du graphe sont appelés des sommets (ou nœuds).
Une relation entre deux sommets est :
- Une arête dans un graphe non-orienté (relation symétrique).
- Un arc dans un graphe orienté (relation à un sens, représentée par une flèche).
Le degré d'un sommet est le nombre d'arêtes qui lui sont liées.
Un chemin est une suite de sommets reliés par des arêtes/arcs. Si le chemin revient à son point de départ, on parle de cycle.
Un graphe est connexe s'il existe toujours un chemin entre n'importe quelle paire de sommets.

Représentations en machine

Il existe deux méthodes principales pour coder un graphe en informatique :

1. La liste d'adjacence

On associe à chaque sommet la liste de ses voisins (ses successeurs). En Python, on utilise souvent un dictionnaire où les clés sont les sommets et les valeurs sont des listes :

# Liste d'adjacence (Représentée par un dictionnaire)
liste_social = {
    'Alice': ['Bob', 'Charlie', 'Eve'],
    'Bob': ['Alice', 'Eve'],
    'Charlie': ['Alice', 'Eve'],
    'David': ['Franck', 'Grace'],
    'Eve': ['Alice', 'Bob', 'Charlie', 'Heidi'],
    'Franck': ['David', 'Grace'],
    'Grace': ['David', 'Franck'],
    'Heidi': ['Eve']
}

2. La matrice d'adjacence

Il s'agit d'un tableau à deux dimensions (matrice). Si le graphe possède n sommets, la matrice est de taille n*n. La case (i, j) contient 1 s'il existe un lien entre le sommet i et le sommet j, sinon 0.

Exemples :

# L'ordre des lignes/colonnes suit l'ordre alphabétique.
matrice_social = [
    [0, 1, 1, 0, 1, 0, 0, 0], # Alice
    [1, 0, 0, 0, 1, 0, 0, 0], # Bob
    [1, 0, 0, 0, 1, 0, 0, 0], # Charlie
    [0, 0, 0, 0, 0, 1, 1, 0], # David
    [1, 1, 1, 0, 0, 0, 0, 1], # Eve
    [0, 0, 0, 1, 0, 0, 1, 0], # Franck
    [0, 0, 0, 1, 0, 1, 0, 0], # Grace
    [0, 0, 0, 0, 1, 0, 0, 0]  # Heidi
]

# Attention : Dans un graphe orienté, ligne = départ, colonne = arrivée
matrice_web = [
    [0, 1, 0, 0], # ac-nice -> eduscol
    [1, 0, 0, 0], # eduscol -> ac-nice
    [1, 1, 0, 0], # google -> ac-nice, eduscol
    [0, 1, 0, 0]  # site-non-ref -> eduscol
]

Implémentation en Python

Nous allons utiliser la programmation orientée objet pour manipuler un graphe représenté par une liste d'adjacence (via un dictionnaire) :

class Graphe:
    def __init__(self):
        # On utilise un dictionnaire : clé = sommet, valeur = liste des voisins
        self.adjacence = {}

    def ajouter_sommet(self, s):
        if s not in self.adjacence:
            self.adjacence[s] = []

    def ajouter_arete(self, s1, s2):
        # Pour un graphe non-orienté, on ajoute le lien dans les deux sens
        self.ajouter_sommet(s1)
        self.ajouter_sommet(s2)
        self.adjacence[s1].append(s2)
        self.adjacence[s2].append(s1)

    def voisins(self, s):
        return self.adjacence[s]

# Exemple de création d'un réseau social simple
g = Graphe()
g.ajouter_arete('Alice', 'Bob')
g.ajouter_arete('Alice', 'Charlie')
print(g.voisins('Alice')) # Affiche ['Bob', 'Charlie']

Le site du prof

Structures de données